The use of composite concrete-filled steel tubes (CFT) for the columns of frame structures is increasing due to advantages they offer over steel or reinforced concrete members: high stiffness and strength, increased ductility, delayed or prevented buckling, etc. Because of their highly nonlinear behavior, the adequate numerical model needs to address number of phenomena such as nonlinear steel and concrete material behavior, buckling of steel tube, cracking of concrete, etc. From these reasons, work in the topic “CFT column resistance” has two directions. The first one is experimental-theoretical analysis of specific problems related to use of CFT columns in “top-down” construction method. The second direction is numerical analysis of CFT columns in frames.

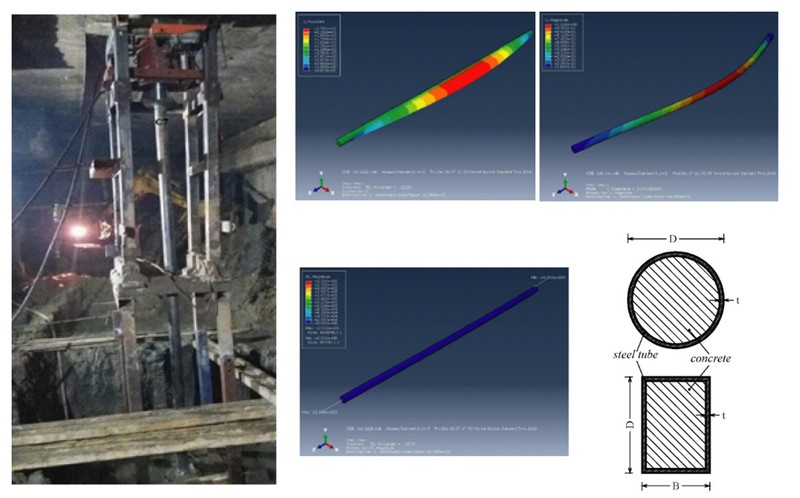
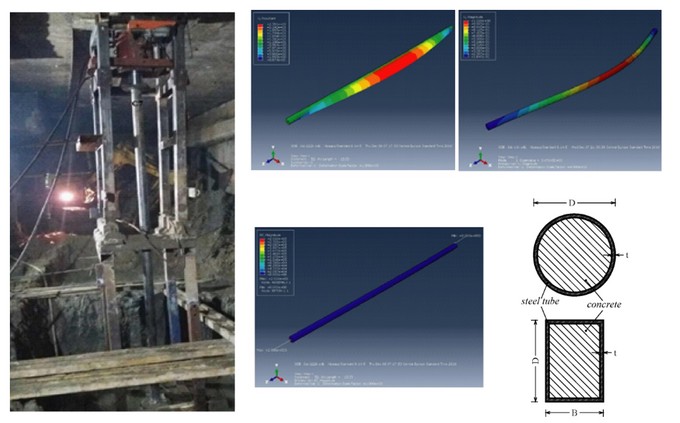
CFT columns found their application in modern "top down" method of construction, where underground part of object is used as strut for supporting peripheral walls and the construction works on the pit protection are performed in parallel with construction of underground part of the object. One important structural member, in this construction method, is the interior ceiling support. These members are usually placed at the position of future columns, and they are constructed as temporary CFT columns. Regarding the capacity of the CFT columns, the critical moment occurs when the excavation reaches the final depth. At that time, the temporary column is subjected to the largest loading from the above part of the structure, and the buckling length of the column is the longest. Resistance of CFT columns under described conditions is experimentally analyzed, on real structure during building. In addition, the problem is numerically studied.

In numerical analysis, these members are modeled either with the 3D solid finite elements in a commercial software (Abaqus), or with the frame elements such as a distributed plasticity fiber beam/column elements and with concentrated plasticity beam/column elements. For analysis of CFT columns, a new nonlinear 3D concentrated plasticity beam–column element is formulated. This element is based on the Generalized Plasticity (GP) material model. It accounts for the interaction between the axial force and the bending moments about the principal axes of the cross section, the gradual yielding of the cross section and the strain hardening response. With the use of the return map algorithm for its state determination, it is computationally efficient. The formulated GP element accounts for the nonlinear geometry under large displacements with the corotational formulation. The model parameters are calibrated from the available experimental results.