Prostorne grede predstavljaju jedan od osnovnih konstruktivnih elemenata u građevinskim konstrukcijama. Upotreba prostornih krivolinijskih grednih elemenata uslovljena je funkcionalnim i estetskim zahtevima. Odgovor ovakvih elemenata na spoljašnje uticaje može se opisati različitim matematičkim modelima tj. teorijama. Jedna od najzastupljenijih teorija grednih nosača je Timošenkova teorija. Kod ovakvog matematičkog modela aksijalne, fleksione i smičuće sile utiču na deformaciju grede. Međutim, kod vitkih greda primetan je efekat nerealno velikog uticaja transferzalnih sila na deformaciju tzv. shear locking. Alternativu pomenutoj teoriji predstavlja Bernuli-Ojlerova teorija kod koje se uticaj smičućih sila na deformaciju zanemaruje čime se ovaj efekat prevazilazi. Proračun prostornih krivolinijskih grednih nosača uglavnom se vrši u programskim paketima koji se baziraju na metodi konačnih elemenata (MKE). Nedostatak direktne veze između postupka za geometrijski opis konstrukcije i postupka analize konstrukcije predstavlja njihov glavni nedostatak. Geometrija konstrukcije se definiše CAD (computer aided-design) programskim paketima koji se baziraju na NURBS (Non Uniform Rational B-Spline) funkcijama. Ove funkcije imaju mogućnost tačnog opisa eliptičnih, paraboličkih i hiperboličkih kontura.

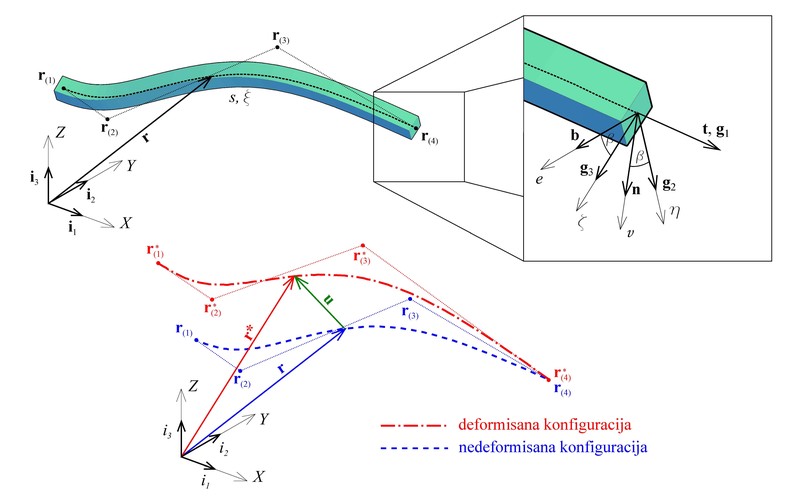
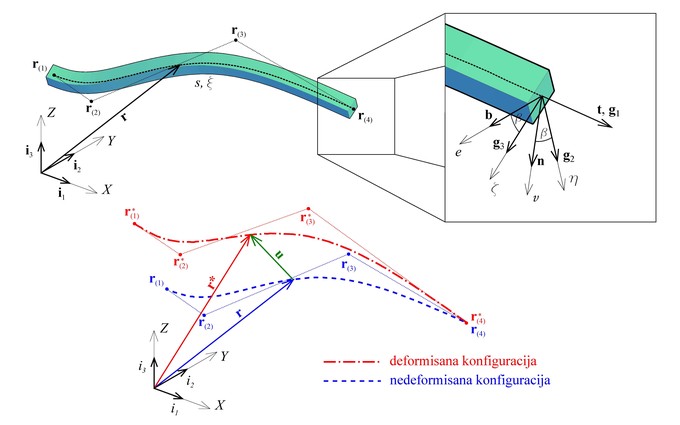
(a) Prostorni krivlinijski gredni nosač, (b) NURBS funkcije
Prvi korak u analizi konstukcija primenom MKE predstavlja fizička diskretizacija konstrukcije, gde se domen konstrukcije deli na manje poddomene - konačne elemente. Ukoliko je neophodno izvršiti usitnjavanje domena, nova fizička diskretizacija domena dobija se iz CAD programskog paketa čime se vreme potrebno za analizu konstrukcije uvećava. Ovaj nedostatak u postupku proračuna konstrukcija predstavlja i glavni motiv za upotrebu izogeometrijskog pristupa u analizi konstrukcija. U izogeometrijskom pristupu, formulacija za opisivanje geometrije koja je definisana CAD programskim paketima koristi se za opisivanje polja pomeranja konstrukcije. Ovakvim pristupom diskretizacija se ne vrši u fizičkom nego u parametarskom domenu. Prednost ovakve formulacije najizraženija je kod prostornog grednog elementa zasnovanog na Bernuli-Ojlerovim pretpostavkama gde su osnovne nepoznate veličine translacije i torziona rotacija poprečnog preseka. Rotacije poprečnog preseka oko glavnih osa inercije nisu stepeni slobode ovakvog sistema, kao što je definisano u klasičnoj MKE, čime se redukuje broj stepeni slobode sistema. Pokazano je da elementi formulisani upotrebom izogeometriskog pristupa daju rezultate visoke tačnosti.
Glavna aktivnost istraživačke grupe vezana je za razvoj izogeometrijskih prostornih krivolinijskih grednih nosača baziranih na različitim teorijama. Fokus je na dinamičkim analizama ovakih elemenata, naročito na uticaju pokretnog opterećenja na konstrukciju. Jedan od ciljeva istraživačke grupe je i razvoj sopstvenog softvera za analizu prostornih krivolinijskih greda u programskom paketu MATLAB baziranog na pomenutim teorijama i principima.

Prva tri oblika oscilovanja obostrano uklještene cilindrične opruge